
Here you will learn how to cut polygons with various algorithms. Remember to use the data structures from the first page, such as Plane, and everything should be in x-z-space (Create a new Vertex object with a Vector3 as its position and where y = 0).
You can use the Sutherland–Hodgman algorithm if you have a polygon and you want to cut away the parts of that polygon that doesn't intersect with another convex polygon. As seen in the Wikipedia article, the polygon you want to cut doesn't have to be convex. This algorithm is best explained in this YouTube video: Sutherland-Hodgman Polygon Clipping Algorithm.
The algorithm assumes that you have sorted the vertices counter-clockwise, so you can travel along the list you send to the algorithm and you will end up at the beginning of the polygon. So you can't just send it random vertices. It is also assumed that you know how to find out if a point is to the left or to the right of a plane (which is the same as finding the distance to the plane), how to find the intersection point between a ray and a plane, and that you know how to clamp a list. If not, you can find the algortihms here: Useful Algorithms.
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public static class SutherlandHodgman
{
//Assumes the polygons are oriented counter clockwise
//poly_1 is the polygon we want to cut
//Assumes the polygon we want to remove from the other polygon is convex, so poly_2 has to be convex
//We will end up with the intersection of the polygons
public static List<Vector3> ClipPolygon(List<Vector3> poly_1, List<Vector3> poly_2)
{
//Calculate the clipping planes
List<Plane> clippingPlanes = new List<Plane>();
for (int i = 0; i < poly_2.Count; i++)
{
int iPlusOne = MathUtility.ClampListIndex(i + 1, poly_2.Count);
Vector3 v1 = poly_2[i];
Vector3 v2 = poly_2[iPlusOne];
//Doesnt have to be center but easier to debug
Vector3 planePos = (v1 + v2) * 0.5f;
Vector3 planeDir = v2 - v1;
//Should point inwards
Vector3 planeNormal = new Vector3(-planeDir.z, 0f, planeDir.x).normalized;
//Gizmos.DrawRay(planePos, planeNormal * 0.1f);
clippingPlanes.Add(new Plane(planePos, planeNormal));
}
List<Vector3> vertices = ClipPolygon(poly_1, clippingPlanes);
return vertices;
}
//Sometimes its more efficient to calculate the planes once before we call the method
//if we want to cut several polygons with the same planes
public static List<Vector3> ClipPolygon(List<Vector3> poly_1, List<Plane> clippingPlanes)
{
//Clone the vertices because we will remove vertices from this list
List<Vector3> vertices = new List<Vector3>(poly_1);
//Save the new vertices temporarily in this list before transfering them to vertices
List<Vector3> vertices_tmp = new List<Vector3>();
//Clip the polygon
for (int i = 0; i < clippingPlanes.Count; i++)
{
Plane plane = clippingPlanes[i];
for (int j = 0; j < vertices.Count; j++)
{
int jPlusOne = MathUtility.ClampListIndex(j + 1, vertices.Count);
Vector3 v1 = vertices[j];
Vector3 v2 = vertices[jPlusOne];
//Calculate the distance to the plane from each vertex
//This is how we will know if they are inside or outside
//If they are inside, the distance is positive, which is why the planes normals have to be oriented to the inside
float dist_to_v1 = Geometry.DistanceFromPointToPlane(plane.normal, plane.pos, v1);
float dist_to_v2 = Geometry.DistanceFromPointToPlane(plane.normal, plane.pos, v2);
//Case 1. Both are outside (= to the right), do nothing
//Case 2. Both are inside (= to the left), save v2
if (dist_to_v1 > 0f && dist_to_v2 > 0f)
{
vertices_tmp.Add(v2);
}
//Case 3. Outside -> Inside, save intersection point and v2
else if (dist_to_v1 < 0f && dist_to_v2 > 0f)
{
Vector3 rayDir = (v2 - v1).normalized;
Vector3 intersectionPoint = Intersections.GetRayPlaneIntersectionCoordinate(plane.pos, plane.normal, v1, rayDir);
vertices_tmp.Add(intersectionPoint);
vertices_tmp.Add(v2);
}
//Case 4. Inside -> Outside, save intersection point
else if (dist_to_v1 > 0f && dist_to_v2 < 0f)
{
Vector3 rayDir = (v2 - v1).normalized;
Vector3 intersectionPoint = Intersections.GetRayPlaneIntersectionCoordinate(plane.pos, plane.normal, v1, rayDir);
vertices_tmp.Add(intersectionPoint);
}
}
//Add the new vertices to the list of vertices
vertices.Clear();
vertices.AddRange(vertices_tmp);
vertices_tmp.Clear();
}
return vertices;
}
}
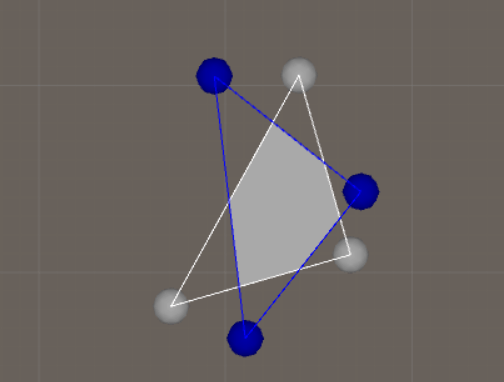
The reason that there's two methods is that it is sometimes more efficient to create the list with clipping planes once if we for example want to cut several polygons with one polygon. This will be useful when we create a Voronoi diagram. The image below shows the result when you clip two triangles. The blue and gray spheres are the positions you store as Vector3 in a list and that you send to the algorithm.
The Sutherland-Hodgman algorithm was kinda limited - it could only find the intersection of two polygons and one of the polygons had to be convex. If you have concave polygons (or convex or one of each) and you want do do other types of so-called boolean operations on the polygons, then you need another algortihm. One such algortihm is the Greiner-Hormann algortihm, and it was presented in the report Efficient clipping of arbitrary polygons which you should read.
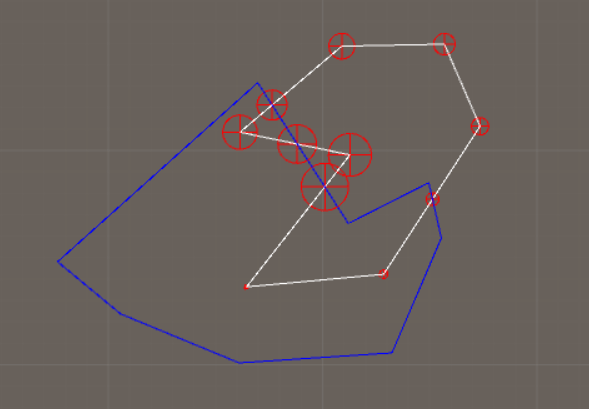
The idea behind the algorithm is that the vertices of the polygons should be arranged counter-clockwise. Then you need to find the intersection points between the edges that goes between the vertices and insert the intersections as new vertices between the old vertices in the original list. Because the intersection points are the same for both the polygon (white) and the clipping-polygon (blue) we might as well modify the clipping-polygon's vertex list and connect these vertices so they are aware of each other. So each intersection point has two vertices - one for each polygon - and they are connected to each other:
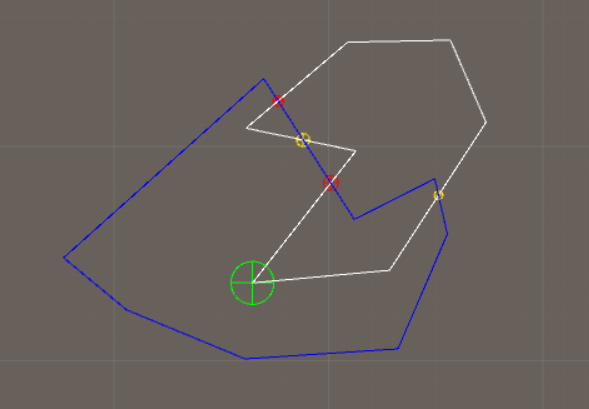
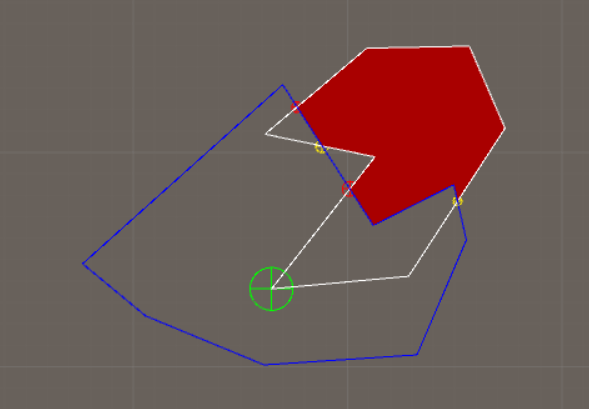
Next step is to figure out if the intersection-vertices are entry points or exit points. In the image below, if we look at the white polygon which is the main polygon (the blue polygon is the clipping-polygon) and look at the first vertex in that white polygon (the big green circle), we can see that it's inside of the blue polygon. If we travel along this polygon (counter-clockwise) we will encounter an intersection-vertex and we need to know if this is an entry or an exit-vertex. Because we started inside of the polygon, we know this has to be an exit-vertex (yellow), and we are now outside of the polygon. Because we are now outside we know the next intersection-vertex we encounter has to be an entry-vertex (red). Also the entry-exit-vertices belonging to the clipping-polygon have to be determined.
Now we can do boolean operations on these polygons, so add the following code:
//Different boolean operations
//Intersection - Remove everything except where both A and B intersect
//Difference - Remove from A where B intersect with A. Remove everything from B
//ExclusiveOr - Remove from A and B where A and B intersect
//Union - Combine A and B into one. Keep everything from A and B
public enum BooleanOperation { Intersection, Difference, ExclusiveOr, Union }
To get the intersection of the two polygons, we should start at the first entry-vertex of the white polygon and move forward until we encounter an exit-vertex. When that happens we should change polygon and instead travel along the clipping-polygon until we find another entry/exit-vertex or are back where we started. This process is repeated until we have visited all entry-vertices.
If we do another boolean operation on the polygons, such as the difference, we just travel in the opposite direction. To get the union of the polygons, we need to do this three times: find the intersection of the polygon and the clipping-polygon, find the difference of the polygon and the clipping-polygon, and find the difference of the clipping-polygon and the polygon. Then we just combine them into one large list of polygons.
This is the intersection between the polygons:
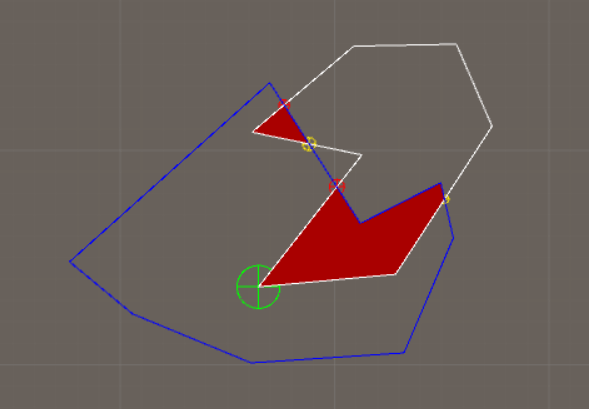
This is the difference:
This is the ExclusiveOr:

This is the union:

To make this work you need to know if a point is in a polygon, how to clamp a list index, and how to tell if two line segments are intersecting and get the intersection point if they are intersecting. If not, you can find the algortihms here: Useful Algorithms.
We also need a class with the same data structure as in the report:
//Same structure as in the report
public class ClipVertex
{
public Vector2 coordinate;
//Next and previous vertex in the chain that will form a polygon if we walk around it
public ClipVertex next;
public ClipVertex prev;
//We may end up with more than one polygon, and this means we jump to that polygon from this polygon
public ClipVertex nextPoly;
//True if this is an intersection vertex
public bool isIntersection = false;
//Is an intersect an entry to a neighbor polygon, otherwise its an exit from a polygon
public bool isEntry;
//If this is an intersection vertex, then this is the same intersection vertex but on the other polygon
public ClipVertex neighbor;
//HIf this is an intersection vertex, this is how far is is between two vertices that are not intersecting
public float alpha = 0f;
//Is this vertex taken by the final polygon, which is more efficient than removing from a list
//when we create the final polygon
public bool isTakenByFinalPolygon;
public ClipVertex(Vector2 coordinate)
{
this.coordinate = coordinate;
}
}
...and this is the main algorithm:
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
//From the report "Efficient clipping of arbitrary polygons"
//Assumes there are no degeneracies (each vertex of one polygon does not lie on an edge of the other polygon)
public static class GreinerHormann
{
public static List<List<Vector2>> ClipPolygons(List<Vector2> polyVector, List<Vector2> clipPolyVector, BooleanOperation booleanOperation)
{
List<List<Vector2>> finalPoly = new List<List<Vector2>>();
//Step 0. Create the data structure needed
List<ClipVertex> poly = InitDataStructure(polyVector);
List<<ClipVertex> clipPoly = InitDataStructure(clipPolyVector);
//Step 1. Find intersection points
//Need to test if we have found an intersection point, if none is found, the polygons dont intersect, or one polygon is inside the other
bool hasFoundIntersection = false;
for (int i = 0; i < poly.Count; i++)
{
ClipVertex currentVertex = poly[i];
//Important to use iPlusOne because poly.next may change
int iPlusOne = MathUtility.ClampListIndex(i + 1, poly.Count);
Vector2 a = poly[i].coordinate;
Vector2 b = poly[iPlusOne].coordinate;
for (int j = 0; j < clipPoly.Count; j++)
{
int jPlusOne = MathUtility.ClampListIndex(j + 1, clipPoly.Count);
Vector2 c = clipPoly[j].coordinate;
Vector2 d = clipPoly[jPlusOne].coordinate;
//Are these lines intersecting?
if (Intersections.AreLinesIntersecting(a, b, c, d, true))
{
hasFoundIntersection = true;
Vector2 intersectionPoint2D = Intersections.GetLineLineIntersectionPoint(a, b, c, d);
//We need to insert this intersection vertex into both polygons
//Insert into the polygon
ClipVertex vertexOnPolygon = InsertIntersectionVertex(a, b, intersectionPoint2D, currentVertex);
//Insert into the clip polygon
ClipVertex vertexOnClipPolygon = InsertIntersectionVertex(c, d, intersectionPoint2D, clipPoly[j]);
//Also connect the intersection vertices with each other
vertexOnPolygon.neighbor = vertexOnClipPolygon;
vertexOnClipPolygon.neighbor = vertexOnPolygon;
}
}
}
//If the polygons are intersecting
if (hasFoundIntersection)
{
//Step 2. Trace each polygon and mark entry and exit points to the other polygon's interior
MarkEntryExit(poly, clipPolyVector);
MarkEntryExit(clipPoly, polyVector);
//Step 3. Create the desired clipped polygon
if (booleanOperation == BooleanOperation.Intersection)
{
//Where the two polygons intersect
List<ClipVertex> intersectionVertices = GetClippedPolygon(poly, true);
AddPolygonToList(intersectionVertices, finalPoly, false);
}
else if (booleanOperation == BooleanOperation.Difference)
{
//Whats outside of the polygon that doesnt intersect
List<ClipVertex> outsidePolyVertices = GetClippedPolygon(poly, false);
AddPolygonToList(outsidePolyVertices, finalPoly, true);
}
else if (booleanOperation == BooleanOperation.ExclusiveOr)
{
//Whats outside of the polygon that doesnt intersect
List<ClipVertex> outsidePolyVertices = GetClippedPolygon(poly, false);
AddPolygonToList(outsidePolyVertices, finalPoly, true);
//Whats outside of the polygon that doesnt intersect
List<ClipVertex> outsideClipPolyVertices = GetClippedPolygon(clipPoly, false);
AddPolygonToList(outsideClipPolyVertices, finalPoly, true);
}
else if (booleanOperation == BooleanOperation.Union)
{
//Where the two polygons intersect
List<ClipVertex> intersectionVertices = GetClippedPolygon(poly, true);
AddPolygonToList(intersectionVertices, finalPoly, false);
//Whats outside of the polygon that doesnt intersect
List<ClipVertex> outsidePolyVertices = GetClippedPolygon(poly, false);
AddPolygonToList(outsidePolyVertices, finalPoly, true);
//Whats outside of the polygon that doesnt intersect
List<ClipVertex> outsideClipPolyVertices = GetClippedPolygon(clipPoly, false);
AddPolygonToList(outsideClipPolyVertices, finalPoly, true);
}
}
//Check if one polygon is inside the other
else
{
//Is the polygon inside the clip polygon?
//Depending on the type of boolean operation, we might get a hole
if (IsPolygonInsidePolygon(polyVector, clipPolyVector))
{
Debug.Log("Poly is inside clip poly");
}
else if (IsPolygonInsidePolygon(clipPolyVector, polyVector))
{
Debug.Log("Clip poly is inside poly");
}
else
{
Debug.Log("Polygons are not intersecting");
}
}
return finalPoly;
}
//We may end up with several polygons, so this will split the connected list into one list per polygon
private static void AddPolygonToList(List<ClipVertex> verticesToAdd, List<List<Vector2>> finalPoly, bool shouldReverse)
{
List<Vector2> thisPolyList = new List<Vector2>();
finalPoly.Add(thisPolyList);
for (int i = 0; i < verticesToAdd.Count; i++)
{
ClipVertex v = verticesToAdd[i];
thisPolyList.Add(v.coordinate);
//Have we found a new polygon?
if (v.nextPoly != null)
{
//If we are finding the !intersection, the vertices will be clockwise
//so we should reverse the list to make it easier to triangulate
if (shouldReverse)
{
thisPolyList.Reverse();
}
thisPolyList = new List();
finalPoly.Add(thisPolyList);
}
}
//Reverse the last list added
if (shouldReverse)
{
finalPoly[finalPoly.Count - 1].Reverse();
}
}
//Get the clipped polygons: either the intersection or the !intersection
//We might end up with more than one polygon and they are connected via clipvertex nextpoly
private static List<ClipVertex> GetClippedPolygon(List<ClipVertex> poly, bool getIntersectionPolygon)
{
List<ClipVertex> finalPolygon = new List<ClipVertex>();
//First we have to reset in case we are repeating this method several times depending on the type of boolean operation
ResetVertices(poly);
//Find the first intersection point which is always where we start
ClipVertex thisVertex = FindFirstEntryVertex(poly);
//Save this so we know when to stop the algortihm
ClipVertex firstVertex = thisVertex;
finalPolygon.Add(thisVertex);
thisVertex.isTakenByFinalPolygon = true;
thisVertex.neighbor.isTakenByFinalPolygon = true;
//These rows is the only part thats different if we want to get the intersection or the !intersection
//Are needed once again if there are more than one polygon
bool isMovingForward = getIntersectionPolygon ? true : false;
thisVertex = getIntersectionPolygon ? thisVertex.next : thisVertex.prev;
int safety = 0;
while (true)
{
//This means we are back at the first vertex of this polygon
if (thisVertex.Equals(firstVertex) || (thisVertex.neighbor != null && thisVertex.neighbor.Equals(firstVertex)))
{
//Try to find the next intersection point in case we end up with more than one polygon
ClipVertex nextVertex = FindFirstEntryVertex(poly);
//Stop if we are out of intersection vertices
if (nextVertex == null)
{
//Debug.Log("No more polygons can be found");
break;
}
//Find an entry vertex and start over with another polygon
else
{
//Debug.Log("Find another polygon");
//Need to connect the polygons
finalPolygon[finalPolygon.Count - 1].nextPoly = nextVertex;
//Change to a new polygon
thisVertex = nextVertex;
firstVertex = nextVertex;
finalPolygon.Add(thisVertex);
thisVertex.isTakenByFinalPolygon = true;
thisVertex.neighbor.isTakenByFinalPolygon = true;
//Do we want to get the intersection or the !intersection
isMovingForward = getIntersectionPolygon ? true : false;
thisVertex = getIntersectionPolygon ? thisVertex.next : thisVertex.prev;
}
}
//If this is not an intersection, then just add it
if (!thisVertex.isIntersection)
{
finalPolygon.Add(thisVertex);
//And move in the direction we are moving
thisVertex = isMovingForward ? thisVertex.next : thisVertex.prev;
}
else
{
thisVertex.isTakenByFinalPolygon = true;
thisVertex.neighbor.isTakenByFinalPolygon = true;
//Jump to the other polygon
thisVertex = thisVertex.neighbor;
finalPolygon.Add(thisVertex);
//Move forward/ back depending on if this is an entry / exit vertex and if we want to find the intersection or not
if (getIntersectionPolygon)
{
isMovingForward = thisVertex.isEntry ? true : false;
thisVertex = thisVertex.isEntry ? thisVertex.next : thisVertex.prev;
}
else
{
isMovingForward = !isMovingForward;
thisVertex = isMovingForward ? thisVertex.next : thisVertex.prev;
}
}
safety += 1;
if (safety > 100000)
{
Debug.Log("Endless loop when creating clipped polygon");
break;
}
}
return finalPolygon;
}
//Reset vertices before we find the final polygon(s)
private static void ResetVertices(List<ClipVertex> poly)
{
ClipVertex resetVertex = poly[0];
int safety = 0;
while (true)
{
//Reset
resetVertex.isTakenByFinalPolygon = false;
resetVertex.nextPoly = null;
//Dont forget to reset the neighbor
if (resetVertex.isIntersection)
{
resetVertex.neighbor.isTakenByFinalPolygon = false;
}
resetVertex = resetVertex.next;
//All vertices are reset
if (resetVertex.Equals(poly[0]))
{
break;
}
safety += 1;
if (safety > 100000)
{
Debug.Log("Endless loop in reset vertices");
break;
}
}
}
//Is a polygon One inside polygon Two?
private static bool IsPolygonInsidePolygon(List<Vector2> polyOne, List<Vector2> polyTwo)
{
bool isInside = false;
for (int i = 0; i < polyOne.Count; i++)
{
if (Intersections.IsPointInPolygon(polyTwo, polyOne[i]))
{
//Is inside if at least one point is inside the polygon (in this case because we run this method after we have tested
//if the polygons are intersecting)
isInside = true;
break;
}
}
return isInside;
}
//Find the the first entry vertex in a polygon
private static ClipVertex FindFirstEntryVertex(List<ClipVertex> poly)
{
ClipVertex thisVertex = poly[0];
ClipVertex firstVertex = thisVertex;
int safety = 0;
while (true)
{
//Is this an available entry vertex?
if (thisVertex.isIntersection && thisVertex.isEntry && !thisVertex.isTakenByFinalPolygon)
{
//We have found the first entry vertex
break;
}
thisVertex = thisVertex.next;
//We have travelled the entire polygon without finding an available entry vertex
if (thisVertex.Equals(firstVertex))
{
thisVertex = null;
break;
}
safety += 1;
if (safety > 100000)
{
Debug.Log("Endless loop in find first entry vertex");
break;
}
}
return thisVertex;
}
//Create the data structure needed
private static List<ClipVertex> InitDataStructure(List<Vector2> polyVector)
{
List<ClipVertex> poly = new List<ClipVertex>();
for (int i = 0; i < polyVector.Count; i++)
{
poly.Add(new ClipVertex(polyVector[i]));
}
//Connect the vertices
for (int i = 0; i < poly.Count; i++)
{
int iPlusOne = MathUtility.ClampListIndex(i + 1, poly.Count);
int iMinusOne = MathUtility.ClampListIndex(i - 1, poly.Count);
poly[i].next = poly[iPlusOne];
poly[i].prev = poly[iMinusOne];
}
return poly;
}
//Insert intersection vertex at correct position in the list
private static ClipVertex InsertIntersectionVertex(Vector2 a, Vector2 b, Vector2 intersectionPoint, ClipVertex currentVertex)
{
//Calculate alpha which is how far the intersection coordinate is between a and b
//so we can insert this vertex at the correct position
//pos = start + dir * alpha
float alpha = (a - intersectionPoint).sqrMagnitude / (a - b).sqrMagnitude;
//Create a new vertex
ClipVertex intersectionVertex = new ClipVertex(intersectionPoint);
intersectionVertex.isIntersection = true;
intersectionVertex.alpha = alpha;
//Now we need to insert this intersection point somewhere after currentVertex
ClipVertex insertAfterThisVertex = currentVertex;
int safety = 0;
while (true)
{
//If the next vertex is an intersectionvertex with a higher alpha
//or if the next vertex is not an intersectionvertex, we cant improve, so break
if (insertAfterThisVertex.next.alpha > alpha || !insertAfterThisVertex.next.isIntersection)
{
break;
}
insertAfterThisVertex = insertAfterThisVertex.next;
safety += 1;
if (safety > 100000)
{
Debug.Log("Stuck in loop in insert intersection vertices");
break;
}
}
//Connect the vertex to the surrounding vertices
intersectionVertex.next = insertAfterThisVertex.next;
intersectionVertex.prev = insertAfterThisVertex;
insertAfterThisVertex.next.prev = intersectionVertex;
insertAfterThisVertex.next = intersectionVertex;
return intersectionVertex;
}
//Mark entry exit points
private static void MarkEntryExit(List<ClipVertex> poly, List<Vector2> clipPolyVector)
{
//First see if the first vertex starts inside or outside (we can use the original list)
bool isInside = Intersections.IsPointInPolygon(clipPolyVector, poly[0].coordinate);
ClipVertex currentVertex = poly[0];
ClipVertex firstVertex = currentVertex;
int safety = 0;
while (true)
{
if (currentVertex.isIntersection)
{
//If we were outside, this is an entry
currentVertex.isEntry = isInside ? false : true;
//Now we know we are either inside or outside
isInside = !isInside;
}
currentVertex = currentVertex.next;
//We have travelled around the entire polygon
if (currentVertex.Equals(firstVertex))
{
break;
}
safety += 1;
if (safety > 100000)
{
Debug.Log("Endless loop in mark entry exit");
break;
}
}
}
}
The problem with this algorithm is that it will fail if one vertex belonging to one polygon is exactly on an edge belonging to the other polygon. To solve this you can modify the algorithm as described in the report "Clipping of Arbitrary Polygons with Degeneracies". But some say that paper doesnt cover all cases, so another similar solution to the Greiner-Hormann algorithm is an algorthm described in the paper "A new algortihm for computing Boolean operations on polygons" which I may implement in the future.