
A Voronoi Diagram is a pattern that looks like the skin of a giraffe. It consists of sites (if you are standing in a cell, then you are closer to this site than any other site in the diagram), cells, and edges. Each site has a cell and the border of the cell is the edges. If you are standing on an edge, you have the same distance to travel to the two sites that are on each side of the edge.
As usual there are more than one way to create a Voronoi Diagram, and we are here going to use two algorithms: An incremental algorithm where we add one site at a time and an algorithm that finds the voronoi diagram by using the delaunay triangulation.We have earlier learned to triangulate random points with the delaunay triangulation algorithm and we can actually use the delaunay triangulation to find the voronoi diagram. To make this work you need to add 4 extra points outside of the random points (one above, one below, one to the left and one to the right) because some voronoi cells are infinite large. By adding 4 extra points and zoom in in the middle then it will look like some voronoi cells are infinite. It will look like this:

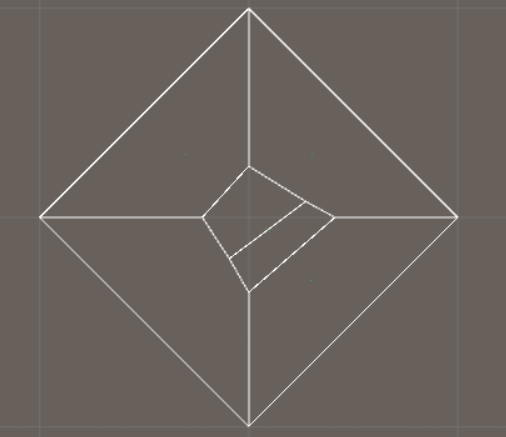
And here you can maybe see the similarities between delaunay and voronoi


This is the main class which you should add to an empty gameobject.
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class VoronoiController : MonoBehaviour
{
public int seed = 0;
public float halfMapSize = 10f;
public float numberOfPoints = 20;
private void OnDrawGizmos()
{
//Generate the random sites
List<Vector3> randomSites = new List<Vector3>();
//Generate random numbers with a seed
Random.InitState(seed);
float max = halfMapSize;
float min = -halfMapSize;
for (int i = 0; i < numberOfPoints; i++)
{
float randomX = Random.Range(min, max);
float randomZ = Random.Range(min, max);
randomSites.Add(new Vector3(randomX, 0f, randomZ));
}
//Points outside of the screen for voronoi which has some cells that are infinite
float bigSize = halfMapSize * 5f;
//Star shape which will give a better result when a cell is infinite large
//When using other shapes, some of the infinite cells misses triangles
randomSites.Add(new Vector3(0f, 0f, bigSize));
randomSites.Add(new Vector3(0f, 0f, -bigSize));
randomSites.Add(new Vector3(bigSize, 0f, 0f));
randomSites.Add(new Vector3(-bigSize, 0f, 0f));
//Generate the voronoi diagram
List<VoronoiCell> cells = DelaunayToVoronoi.GenerateVoronoiDiagram(randomSites);
//Debug
//Display the voronoi diagram
DisplayVoronoiCells(cells);
//Display the sites
Gizmos.color = Color.white;
for (int i = 0; i < randomSites.Count; i++)
{
float radius = 0.2f;
Gizmos.DrawSphere(randomSites[i], radius);
}
}
//Display the voronoi diagram with mesh
private void DisplayVoronoiCells(List<VoronoiCell> cells)
{
Random.InitState(seed);
for (int i = 0; i < cells.Count; i++)
{
VoronoiCell c = cells[i];
Vector3 p1 = c.sitePos;
Gizmos.color = new Color(Random.Range(0f, 1f), Random.Range(0f, 1f), Random.Range(0f, 1f), 1f);
List<Vector3> vertices = new List<Vector3>();
List<int> triangles = new List<int>();
vertices.Add(p1);
for (int j = 0; j < c.edges.Count; j++)
{
Vector3 p3 = c.edges[j].v1;
Vector3 p2 = c.edges[j].v2;
vertices.Add(p2);
vertices.Add(p3);
triangles.Add(0);
triangles.Add(vertices.Count - 2);
triangles.Add(vertices.Count - 1);
}
Mesh triangleMesh = new Mesh();
triangleMesh.vertices = vertices.ToArray();
triangleMesh.triangles = triangles.ToArray();
triangleMesh.RecalculateNormals();
Gizmos.DrawMesh(triangleMesh);
}
}
}
These are the classes that will take care of the construction of the voronoi diagram. Make sure you've the code from the delaunay triangulation.
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
//From https://stackoverflow.com/questions/85275/how-do-i-derive-a-voronoi-diagram-given-its-point-set-and-its-delaunay-triangula
public class DelaunayToVoronoi
{
public static List<VoronoiCell> GenerateVoronoiDiagram(List<Vector3> sites)
{
//First generate the delaunay triangulation
List<Triangle> triangles = Delaunay.TriangulateByFlippingEdges(sites);
//Generate the voronoi diagram
//Step 1. For every delaunay edge, compute a voronoi edge
//The voronoi edge is the edge connecting the circumcenters of two neighboring delaunay triangles
List<VoronoiEdge> voronoiEdges = new List<VoronoiEdge>();
for (int i = 0; i < triangles.Count; i++)
{
Triangle t = triangles[i];
//Each triangle consists of these edges
HalfEdge e1 = t.halfEdge;
HalfEdge e2 = e1.nextEdge;
HalfEdge e3 = e2.nextEdge;
//Calculate the circumcenter for this triangle
Vector3 v1 = e1.v.position;
Vector3 v2 = e2.v.position;
Vector3 v3 = e3.v.position;
//The circumcenter is the center of a circle where the triangles corners is on the circumference of that circle
//The .XZ() is an extension method that removes the y value of a vector3 so it becomes a vector2
Vector2 center2D = Geometry.CalculateCircleCenter(v1.XZ(), v2.XZ(), v3.XZ());
//The circumcenter is also known as a voronoi vertex, which is a position in the diagram where we are equally
//close to the surrounding sites
Vector3 voronoiVertex = new Vector3(center2D.x, 0f, center2D.y);
TryAddVoronoiEdgeFromTriangleEdge(e1, voronoiVertex, voronoiEdges);
TryAddVoronoiEdgeFromTriangleEdge(e2, voronoiVertex, voronoiEdges);
TryAddVoronoiEdgeFromTriangleEdge(e3, voronoiVertex, voronoiEdges);
}
//Step 2. Find the voronoi cells where each cell is a list of all edges belonging to a site
List<VoronoiCell> voronoiCells = new List<VoronoiCell>();
for (int i = 0; i < voronoiEdges.Count; i++)
{
VoronoiEdge e = voronoiEdges[i];
//Find the position in the list of all cells that includes this site
int cellPos = TryFindCellPos(e, voronoiCells);
//No cell was found so we need to create a new cell
if (cellPos == -1)
{
VoronoiCell newCell = new VoronoiCell(e.sitePos);
voronoiCells.Add(newCell);
newCell.edges.Add(e);
}
else
{
voronoiCells[cellPos].edges.Add(e);
}
}
return voronoiCells;
}
//Find the position in the list of all cells that includes this site
//Returns -1 if no cell is found
private static int TryFindCellPos(VoronoiEdge e, List<VoronoiCell> voronoiCells)
{
for (int i = 0; i < voronoiCells.Count; i++)
{
if (e.sitePos == voronoiCells[i].sitePos)
{
return i;
}
}
return -1;
}
//Try to add a voronoi edge. Not all edges have a neighboring triangle, and if it hasnt we cant add a voronoi edge
private static void TryAddVoronoiEdgeFromTriangleEdge(HalfEdge e, Vector3 voronoiVertex, List<VoronoiEdge> allEdges)
{
//Ignore if this edge has no neighboring triangle
if (e.oppositeEdge == null)
{
return;
}
//Calculate the circumcenter of the neighbor
HalfEdge eNeighbor = e.oppositeEdge;
Vector3 v1 = eNeighbor.v.position;
Vector3 v2 = eNeighbor.nextEdge.v.position;
Vector3 v3 = eNeighbor.nextEdge.nextEdge.v.position;
//The .XZ() is an extension method that removes the y value of a vector3 so it becomes a vector2
Vector2 center2D = Geometry.CarculateCircleCenter(v1.XZ(), v2.XZ(), v3.XZ());
Vector3 voronoiVertexNeighbor = new Vector3(center2D.x, 0f, center2D.y);
//Create a new voronoi edge between the voronoi vertices
VoronoiEdge edge = new VoronoiEdge(voronoiVertex, voronoiVertexNeighbor, e.prevEdge.v.position);
allEdges.Add(edge);
}
}
public class VoronoiEdge
{
//These are the voronoi vertices
public Vector3 v1;
public Vector3 v2;
//All positions within a voronoi cell is closer to this position than any other position in the diagram
public Vector3 sitePos;
public VoronoiEdge(Vector3 v1, Vector3 v2, Vector3 sitePos)
{
this.v1 = v1;
this.v2 = v2;
this.sitePos = sitePos;
}
}
public class VoronoiCell
{
//All positions within a voronoi cell is closer to this position than any other position in the diagram
public Vector3 sitePos;
public List<VoronoiEdge> edges = new List<VoronoiEdge>();
public VoronoiCell(Vector3 sitePos)
{
this.sitePos = sitePos;
}
}
This is how you calculate the circle center if you have three points:
//Calculate the center of circle in 2d space given three coordinates
//http://paulbourke.net/geometry/circlesphere/
public static Vector2 CalculateCircleCenter(Vector2 p1, Vector2 p2, Vector2 p3)
{
Vector2 center = new Vector2();
float ma = (p2.y - p1.y) / (p2.x - p1.x);
float mb = (p3.y - p2.y) / (p3.x - p2.x);
center.x = (ma * mb * (p1.y - p3.y) + mb * (p1.x + p2.x) - ma * (p2.x + p3.x)) / (2 * (mb - ma));
center.y = (-1 / ma) * (center.x - (p1.x + p2.x) / 2) + (p1.y + p2.y) / 2;
return center;
}
If everything is working fine, it should look like this:

I found the idea for this algorithm here Algorithm for generation of Voronoi Diagrams. According to the site you don't need to care about floating point precision, but I discovered that you need because this algortihm will sometimes make some voronoi edges disappear. So the voronoi-from-delaunay algorithm is more stable, but I've kept this algortihm here in case someone needs it. You may use the voronoi-from-delaunay and then this algortihm to add more sites if you need, but then you need to modify the code.
The idea is that we first create 4 fake sites with triangles around them, which looks like this:

...and then we add site-by-site while cutting the existing edges:

...2 sites:
The difficult part here is to cut the edges. The webpage says that we should "Test the spatial relationship between e and pb." This means that we should test on which side an existing edge is in relationship to the perpendicular vector. To make this work, we need to know which side of the perpendicular vector a point is. This means it is really important to orient all perpendicular vectors in the same way - all of them have to point in the same direction. And I've here decided that to the left of the perpendicular vector should the site we want to add be, and to the right should the existing side be.
When we have done that we should be able to answer the following: "If e is on the near side of pb (closer to site than to c's site), mark it to be deleted (or delete it now provided that doing so will not disrupt your enumeration)." This means that if an existing edge is to the left of the perpendicular vector we should delete it. We can also answer: "If e intersects pb, clip e to the far side of pb, and store the point of intersection in X." This means that if an existing edge is intersecting with the perpendicular vector, then we should move what's left of the perpendicular vector to the intersection point. If you head is spinning, this image might explain it:
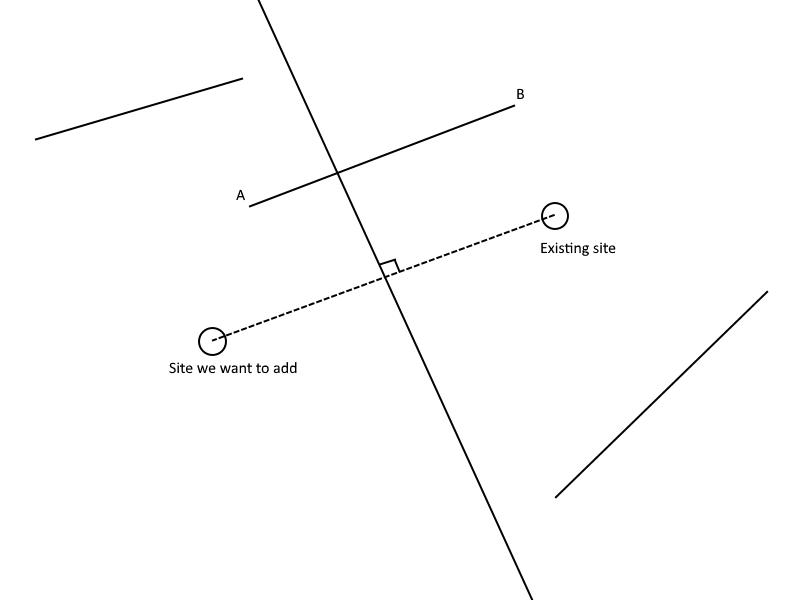
As seen in the image above, we have 3 cases. If the edge is to the left of the line, then delete it. If an edge is to the right of the line, then ignore it. If an edge is intersecting with the line, move vertex A (which is to the left) to the intersection point. This sounds simple inte theory, but fails miserable when implementing it in Unity. The problem is floating point precision issues. When we cut a line, the intersection point will not be exactly where the intersection point is in theory, so to make it work we have to use a tolerance, which I've from experimentation determined that it should be 0.001. So if an edge is to the left or 0.001 to the right of the perpendicular vector, we say the entire edge is to the left and we should delete it.
What has been explained so far is what this code is doing. halfWidth is half of the width of the range your points have. If your points are centered around 0 and no point is larger than 10 nor smaller than -10, then halfWidth is 10:
public static List<Cell> GenerateVoronoiDiagramSiteBySite(List<Vector3> sites, float halfWidth)
{
//Initialize edges and cells to be empty
List<Edge> edges = new List<Edge>();
List<Cell> cells = new List<Cell>();
//
// Step 1. Add three or four "points at infinity" to cells, to bound the diagram
//
float width = halfWidth * 3f;
float bigWidth = halfWidth * 10f;
//Add appropriate edges to these cells - will form a triangle
//And all triangles will form a diamond shape with center at center of points
Vector3 C = new Vector3(0f, 0f, 0f);
Vector3 R = new Vector3(bigWidth, 0f, 0f);
Vector3 T = new Vector3(0f, 0f, bigWidth);
Vector3 L = new Vector3(-bigWidth, 0f, 0f);
Vector3 B = new Vector3(0f, 0f, -bigWidth);
//BL
Cell cell1 = new Cell(new Vector3(-width, 0f, -width));
cell1.edges.Add(new Edge(C, L));
cell1.edges.Add(new Edge(L, B));
cell1.edges.Add(new Edge(B, C));
cells.Add(cell1);
//BR
Cell cell2 = new Cell(new Vector3(width, 0f, -width));
cell2.edges.Add(new Edge(C, B));
cell2.edges.Add(new Edge(B, R));
cell2.edges.Add(new Edge(R, C));
cells.Add(cell2);
//TR
Cell cell3 = new Cell(new Vector3(width, 0f, width));
cell3.edges.Add(new Edge(C, R));
cell3.edges.Add(new Edge(R, T));
cell3.edges.Add(new Edge(T, C));
cells.Add(cell3);
//TL
Cell cell4 = new Cell(new Vector3(-width, 0f, width));
cell4.edges.Add(new Edge(C, T));
cell4.edges.Add(new Edge(T, L));
cell4.edges.Add(new Edge(L, C));
cells.Add(cell4);
//
// Step 2. Add the sites one by one and rebuild the diagram
//
//Loop through all sites we want to add
for (int i = 0; i < sites.Count; i++)
{
//Create a new cell with site as its site
Cell newCell = new Cell(sites[i]);
//For each existing cell
for (int j = 0; j < cells.Count; j++)
{
Cell existingCell = cells[j];
//Find perpendicular bisector of the line segment connecting the two sites
Vector3 vecBetween = (newCell.cellPos - existingCell.cellPos).normalized;
//This direction is always ccw around the site we are adding
Vector3 pbVec = new Vector3(vecBetween.z, 0f, -vecBetween.x);
//The position of this vector
Vector3 centerPos = (newCell.cellPos + existingCell.cellPos) * 0.5f;
//Create a data structure to hold the critical points and edges to delete
List<Vector3> criticalPoints = new List<Vector3>();
List<Edge> edgesToDelete = new List<Edge>();
//Loop through all edges belonging to the current site
for (int k = 0; k < existingCell.edges.Count; k++)
{
Edge edge = existingCell.edges[k];
//Test the spatial relationship between e and pb (determine which side of a line a given point is on)
Vector3 edge_p1 = edge.v1.position;
Vector3 edge_p2 = edge.v2.position;
//If e is on the near side of pb (closer to the new site we are currently adding than to the existing site),
//mark it to be deleted. This means that if the entire line is to the left of the line we are drawing now, delete it
// < 0 -> to the right
// = 0 -> on the line
// > 0 -> to the left
float relation_p1 = Geometry.DistanceFromPointToPlane(vecBetween, centerPos, edge_p1);
float relation_p2 = Geometry.DistanceFromPointToPlane(vecBetween, centerPos, edge_p2);
//Make the edge a little longer because of floating point precisions, or the intersection algortihm will not work
Vector3 edgeDir = (edge_p2 - edge_p1).normalized;
float tolerance = 0.001f;
Vector3 edge_p2_extended = edge_p2 + edgeDir * tolerance;
Vector3 edge_p1_extended = edge_p1 - edgeDir * tolerance;
//Both points are to the left
float left_tolerance = -0.001f;
if ((relation_p1 > 0f && relation_p2 >= left_tolerance) || (relation_p2 > 0f && relation_p1 >= left_tolerance))
{
edgesToDelete.Add(edge);
}
else if (Intersections.AreLinePlaneIntersecting(vecBetween, centerPos, edge_p1_extended, edge_p2_extended))
{
Vector3 intersectionPoint = Intersections.GetLinePlaneIntersectionCoordinate(vecBetween, centerPos, edge_p1, edge_p2);
criticalPoints.Add(intersectionPoint);
//Both points are to the right
if (relation_p1 < 0f && relation_p2 < 0f)
{
//Move the one thats least to the right to the intersection coordinate
if (relation_p1 > relation_p2)
{
edge.v1.position = intersectionPoint;
}
else
{
edge.v2.position = intersectionPoint;
}
}
//The points are on different sides of the line, so move the left one
else if (relation_p1 > 0f || Mathf.Approximately(relation_p1, 0f))
{
edge.v1.position = intersectionPoint;
}
else
{
edge.v2.position = intersectionPoint;
}
}
}
//Critical points should now have 0 or 2 points, if 2 points, add it
if (criticalPoints.Count == 2)
{
Edge newEdge = new Edge(criticalPoints[0], criticalPoints[1]);
//Add this edge to teh lists
existingCell.edges.Add(newEdge);
newCell.edges.Add(newEdge);
edges.Add(newEdge);
}
//Delete the edges we should delete
for (int l = 0; l < edgesToDelete.Count; l++)
{
existingCell.edges.Remove(edgesToDelete[l]);
edges.Remove(edgesToDelete[l]);
}
}
cells.Add(newCell);
}
}
...which assumes you have a Cell class:
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class Cell
{
public Vector3 cellPos;
public List<Edge> edges = new List<Edge>();
//This list should be sorted so we can walk around the cell border
public List<Vector3> borderCoordinates = new List<Vector3>();
public Cell(Vector3 cellPos)
{
this.cellPos = cellPos;
}
}
Remember to use the data structures from the first page, such as Edge, and everything should be in x-z-space (Create a new Vertex object with a Vector3 as its position and where y = 0). You also need to know how to find out if a point is to the left or to the right of a plane, if a line and plane is intersecting, and the coordinate of intersection between a line and plane. If not, you can find them here: Useful Algorithms.
We now have a list with all sites, so we should begin with removing the 4 fake sites we added in the beginning because they are not needed anymore. We also need to connect the edges which belongs to a site, so we can easier cut the fake edges we added in the beginning which now belongs to sites that intersects with the border:

To be able to connect the edges, we first have to make sure they have the same orientation, which is counter-clockwise around the site. So we end up with edges that goes from v1 to v2, but we don't know which edge comes after another edge. What we want a list with coordinates that goes from A-B-C-D-E if we have 5 vertices. To connect the edges we check how close and edge's endpoint (v2) is to another edge's startpoint (v1).
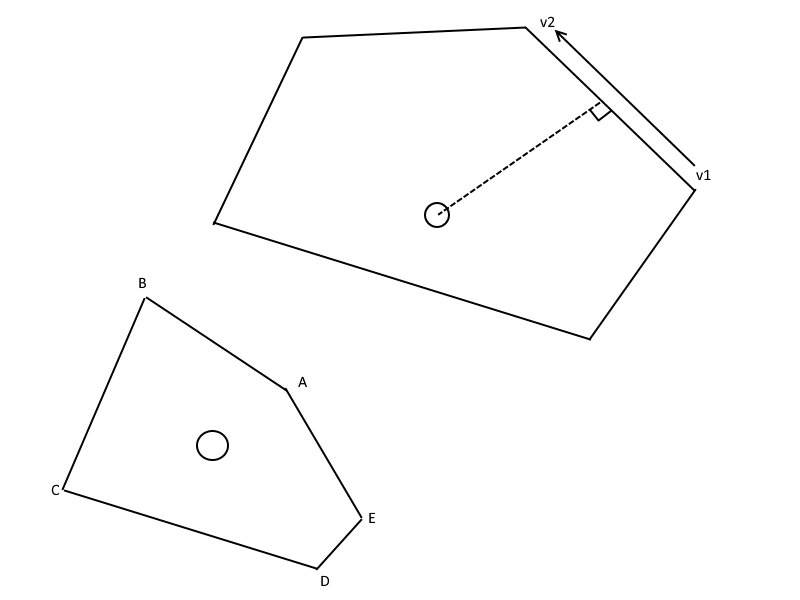
//Remove the first 4 cells we added in the beginning because they are not needed anymore
cells.RemoveRange(0, 4);
for (int i = 0; i < cells.Count; i++)
{
//We should move around the cell counter-clockwise so make sure all edges are oriented in that way
List<Edge> cellEdges = cells[i].edges;
for (int j = cellEdges.Count - 1; j >= 0; j--)
{
Vertex edge_v1 = cellEdges[j].v1;
Vertex edge_v2 = cellEdges[j].v2;
//Remove this edge if it is small
if ((edge_v1.position - edge_v2.position).sqrMagnitude < 0.01f)
{
cellEdges.RemoveAt(j);
continue;
}
Vector3 edgeCenter = (edge_v1.position + edge_v2.position) * 0.5f;
//Now we can make a line between the cell and the edge
Vector2 a = new Vector2(cells[i].cellPos.x, cells[i].cellPos.z);
Vector2 b = new Vector2(edgeCenter.x, edgeCenter.z);
//The point to the left of this line is coming after the other point if we are moving counter-clockwise
if (Geometry.IsAPointLeftOfVector(a, b, edge_v1.GetPos2D_XZ()))
{
//Flip because we want to go from v1 to v2
Vector3 temp = edge_v2.position;
edge_v2.position = edge_v1.position;
edge_v1.position = temp;
}
}
//Connect the edges
List<Vector3> edgesCoordinates = cells[i].borderCoordinates;
Edge startEdge = cellEdges[0];
edgesCoordinates.Add(startEdge.v2.position);
Vertex currentVertex = startEdge.v2;
for (int j = 1; j < cellEdges.Count; j++)
{
//Find the next edge
for (int k = 1; k < cellEdges.Count; k++)
{
Vector3 thisEdgeStart = cellEdges[k].v1.position;
if ((thisEdgeStart - currentVertex.position).sqrMagnitude < 0.01f)
{
edgesCoordinates.Add(cellEdges[k].v2.position);
currentVertex = cellEdges[k].v2;
break;
}
}
}
}
Each cell now has a list called edgesCoordinates. This list is sorted so we can travel around the site (along the edge) and end up at the same position as where we started. We also know that the border of this Voronoi diagram is a square, so we can use the Sutherland-Hodgman algorithm to cut away the fake edges we added in the beginning. This method is doing that:
//Clip the Voronoi diagram with a clipping algorithm which is a better solution than the solution suggested on the webpage
private static void ClipDiagram(List<Cell> cells, float halfWidth)
{
List<Vector3> clipPolygon = new List<Vector3>();
//The positions of the square border
Vector3 TL = new Vector3(-halfWidth, 0f, halfWidth);
Vector3 TR = new Vector3(halfWidth, 0f, halfWidth);
Vector3 BR = new Vector3(halfWidth, 0f, -halfWidth);
Vector3 BL = new Vector3(-halfWidth, 0f, -halfWidth);
clipPolygon.Add(TL);
clipPolygon.Add(BL);
clipPolygon.Add(BR);
clipPolygon.Add(TR);
//Create the clipping planes
List<Plane> clippingPlanes = new List<Plane>();
for (int i = 0; i < clipPolygon.Count; i++)
{
int iPlusOne = MathUtility.ClampListIndex(i + 1, clipPolygon.Count);
Vector3 v1 = clipPolygon[i];
Vector3 v2 = clipPolygon[iPlusOne];
//Doesnt have to be center but easier to debug
Vector3 planePos = (v1 + v2) * 0.5f;
Vector3 planeDir = v2 - v1;
//Should point inwards
Vector3 planeNormal = new Vector3(-planeDir.z, 0f, planeDir.x).normalized;
clippingPlanes.Add(new Plane(planePos, planeNormal));
}
for (int i = 0; i < cells.Count; i++)
{
cells[i].borderCoordinates = SutherlandHodgman.ClipPolygon(cells[i].borderCoordinates, clippingPlanes);
}
}
Each cell now has a list called edgesCoordinates. This list is a convex polygon, so if you want to triangulate it, you can use this algortihm: Triangulate a convex polygon. And we will finally end up with a Voronoi Diagram:
