
Here you will learn everything about how to triangulate a polygon and random points. Remember to use the data structures from the first page, such as Vertex and Triangle, and everything should be in x-z-space (Create a new Vertex object with a Vector3 as its position and where y = 0).
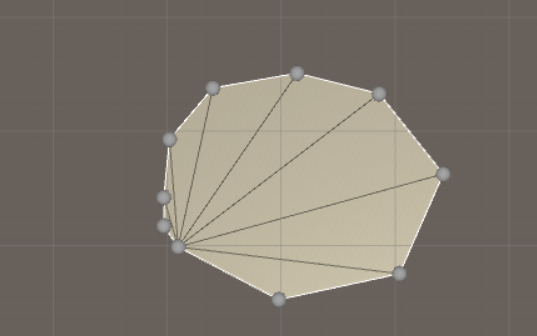
Triangulating a convex polygon is very easy, so we start with that. This algorithms assumes that the vertices you want to triangulate are sorted along the hull of the polygon. If they are not sorted you can use a convex hull algorithm to sort them!
public static List<Triangle> TriangulateConvexPolygon(List<Vertex> convexHullpoints)
{
List<Triangle> triangles = new List<Triangle>();
for (int i = 2; i < convexHullpoints.Count; i++)
{
Vertex a = convexHullpoints[0];
Vertex b = convexHullpoints[i - 1];
Vertex c = convexHullpoints[i];
triangles.Add(new Triangle(a, b, c));
}
return triangles;
}
And this is the result:
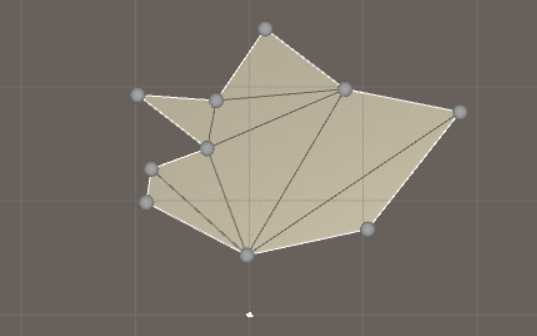
Triangulating a concave polygon is similar to triangulating a convex polygon. There are several algorithms you can use, but we are here going to use an algorithm called ear clipping. It is explained in this pdf: Triangulation by Ear Clipping. The idea is that we identify the polygon's ears (an ear is simply a triangle), and then we cut ears from the polygon until only one triangle is left, and then we have triangulated the polygon.
This assumes you can clamp a list, knows how to tell if a triangle is oriented clockwise, and if a point is in a triangle. If not, you can find the algorithms here: A collection of useful algorithms.
//This assumes that we have a polygon and now we want to triangulate it
//The points on the polygon should be ordered counter-clockwise
//This alorithm is called ear clipping and it's O(n*n) Another common algorithm is dividing it into trapezoids and it's O(n log n)
//One can maybe do it in O(n) time but no such version is known
//Assumes we have at least 3 points
public static List<Triangle> TriangulateConcavePolygon(List<Vector3> points)
{
//The list with triangles the method returns
List<Triangle> triangles = new List<Triangle>();
//If we just have three points, then we dont have to do all calculations
if (points.Count == 3)
{
triangles.Add(new Triangle(points[0], points[1], points[2]));
return triangles;
}
//Step 1. Store the vertices in a list and we also need to know the next and prev vertex
List<Vertex> vertices = new List<Vertex>();
for (int i = 0; i < points.Count; i++)
{
vertices.Add(new Vertex(points[i]));
}
//Find the next and previous vertex
for (int i = 0; i < vertices.Count; i++)
{
int nextPos = MathUtility.ClampListIndex(i + 1, vertices.Count);
int prevPos = MathUtility.ClampListIndex(i - 1, vertices.Count);
vertices[i].prevVertex = vertices[prevPos];
vertices[i].nextVertex = vertices[nextPos];
}
//Step 2. Find the reflex (concave) and convex vertices, and ear vertices
for (int i = 0; i < vertices.Count; i++)
{
CheckIfReflexOrConvex(vertices[i]);
}
//Have to find the ears after we have found if the vertex is reflex or convex
List<Vertex> earVertices = new List<Vertex>();
for (int i = 0; i < vertices.Count; i++)
{
IsVertexEar(vertices[i], vertices, earVertices);
}
//Step 3. Triangulate!
while (true)
{
//This means we have just one triangle left
if (vertices.Count == 3)
{
//The final triangle
triangles.Add(new Triangle(vertices[0], vertices[0].prevVertex, vertices[0].nextVertex));
break;
}
//Make a triangle of the first ear
Vertex earVertex = earVertices[0];
Vertex earVertexPrev = earVertex.prevVertex;
Vertex earVertexNext = earVertex.nextVertex;
Triangle newTriangle = new Triangle(earVertex, earVertexPrev, earVertexNext);
triangles.Add(newTriangle);
//Remove the vertex from the lists
earVertices.Remove(earVertex);
vertices.Remove(earVertex);
//Update the previous vertex and next vertex
earVertexPrev.nextVertex = earVertexNext;
earVertexNext.prevVertex = earVertexPrev;
//...see if we have found a new ear by investigating the two vertices that was part of the ear
CheckIfReflexOrConvex(earVertexPrev);
CheckIfReflexOrConvex(earVertexNext);
earVertices.Remove(earVertexPrev);
earVertices.Remove(earVertexNext);
IsVertexEar(earVertexPrev, vertices, earVertices);
IsVertexEar(earVertexNext, vertices, earVertices);
}
//Debug.Log(triangles.Count);
return triangles;
}
//Check if a vertex if reflex or convex, and add to appropriate list
private static void CheckIfReflexOrConvex(Vertex v)
{
v.isReflex = false;
v.isConvex = false;
//This is a reflex vertex if its triangle is oriented clockwise
Vector2 a = v.prevVertex.GetPos2D_XZ();
Vector2 b = v.GetPos2D_XZ();
Vector2 c = v.nextVertex.GetPos2D_XZ();
if (Geometry.IsTriangleOrientedClockwise(a, b, c))
{
v.isReflex = true;
}
else
{
v.isConvex = true;
}
}
//Check if a vertex is an ear
private static void IsVertexEar(Vertex v, List<Vertex> vertices, List<Vertex> earVertices)
{
//A reflex vertex cant be an ear!
if (v.isReflex)
{
return;
}
//This triangle to check point in triangle
Vector2 a = v.prevVertex.GetPos2D_XZ();
Vector2 b = v.GetPos2D_XZ();
Vector2 c = v.nextVertex.GetPos2D_XZ();
bool hasPointInside = false;
for (int i = 0; i < vertices.Count; i++)
{
//We only need to check if a reflex vertex is inside of the triangle
if (vertices[i].isReflex)
{
Vector2 p = vertices[i].GetPos2D_XZ();
//This means inside and not on the hull
if (Intersections.IsPointInTriangle(a, b, c, p))
{
hasPointInside = true;
break;
}
}
}
if (!hasPointInside)
{
earVertices.Add(v);
}
}
And this is the result:
Let's say you have points in the plane you want to triangulate. According to Wikipedia, there are three algorithms you can use: Triangle Splitting Algorithm, Incremental Algorithm, and Delaunay Triangulation Algorithm. We are in this section going to cover the first two.
Triangle Splitting Algorithm
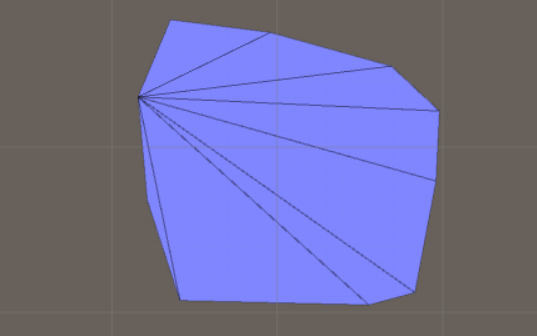
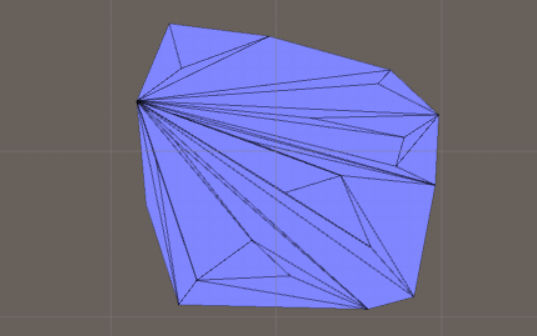
The idea here is that we first find the convex hull of the points, then we use one of the above algorithms to triangulate the convex hull. Now we just add the points that are within the hull one-by-one. Each time we add a new point, we check which triangle it is in, then we split that triangle into three triangles. The result is not pretty but it is a valid triangulation, which is good in most cases!
This assumes you can can tell if a point is in a triangle. If not, you can find the algorithm here: A collection of useful algorithms.
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
//Triangulate random points by first generating the convex hull of the points, then triangulate the convex hull
//and then add the other points and split the triangle the point is in
public static class TriangleSplittingAlgorithm
{
public static List<Triangle> TriangulatePoints(List<Vertex> points)
{
//Generate the convex hull - will also remove the points from points list which are not on the hull
List<Vertex> pointsOnConvexHull = HullAlgorithms.JarvisMarch(points);
//Triangulate the convex hull
List<Triangle> triangles = TriangulateHullAlgorithms.TriangulateConvexPolygon(pointsOnConvexHull);
//Add the remaining points and split the triangles
for (int i = 0; i < points.Count; i++)
{
Vertex currentPoint = points[i];
//2d space
Vector2 p = new Vector2(currentPoint.position.x, currentPoint.position.z);
//Which triangle is this point in?
for (int j = 0; j < triangles.Count; j++)
{
Triangle t = triangles[j];
Vector2 p1 = new Vector2(t.v1.position.x, t.v1.position.z);
Vector2 p2 = new Vector2(t.v2.position.x, t.v2.position.z);
Vector2 p3 = new Vector2(t.v3.position.x, t.v3.position.z);
if (Intersections.IsPointInTriangle(p1, p2, p3, p))
{
//Create 3 new triangles
Triangle t1 = new Triangle(t.v1, t.v2, currentPoint);
Triangle t2 = new Triangle(t.v2, t.v3, currentPoint);
Triangle t3 = new Triangle(t.v3, t.v1, currentPoint);
//Remove the old triangle
triangles.Remove(t);
//Add the new triangles
triangles.Add(t1);
triangles.Add(t2);
triangles.Add(t3);
break;
}
}
}
return triangles;
}
}
And this is the result before we add the interior points:
And this is the final triangulation:
Incremental Algorithm
According to Wikipedia, we should sort the points according to x-coordinates. The first three points determine a triangle. Consider the next point in the ordered set and connect it with all previously considered points which are visible to the point. Continue this process of adding points until all has been processed.
The trick here is how can we say an edge is visible to a point? What I came up with is that we should find the center of an edge belonging to a triangle and connect this center point with the point we want to add. If this edge doesn't intersect another edge, then it's visible. This assumes you can can tell if two lines are intersecting. If not, you can find the algorithm here: A collection of useful algorithms.
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
using System.Linq;
//Sort the points along one axis. The first 3 points form a triangle. Consider the next point and connect it with all
//previously connected points which are visible to the point. An edge is visible if the center of the edge is visible to the point.
public static class IncrementalTriangulationAlgorithm
{
public static List<Triangle> TriangulatePoints(List<Vertex> points)
{
List<Triangle> triangles = new List<Triangle>();
//Sort the points along x-axis
//OrderBy is always soring in ascending order - use OrderByDescending to get in the other order
points = points.OrderBy(n => n.position.x).ToList();
//The first 3 vertices are always forming a triangle
Triangle newTriangle = new Triangle(points[0].position, points[1].position, points[2].position);
triangles.Add(newTriangle);
//All edges that form the triangles, so we have something to test against
List<Edge> edges = new List<Edge>();
edges.Add(new Edge(newTriangle.v1, newTriangle.v2));
edges.Add(new Edge(newTriangle.v2, newTriangle.v3));
edges.Add(new Edge(newTriangle.v3, newTriangle.v1));
//Add the other triangles one by one
//Starts at 3 because we have already added 0,1,2
for (int i = 3; i < points.Count; i++)
{
Vector3 currentPoint = points[i].position;
//The edges we add this loop or we will get stuck in an endless loop
List<Edge> newEdges = new List<Edge>();
//Is this edge visible? We only need to check if the midpoint of the edge is visible
for (int j = 0; j < edges.Count; j++)
{
Edge currentEdge = edges[j];
Vector3 midPoint = (currentEdge.v1.position + currentEdge.v2.position) / 2f;
Edge edgeToMidpoint = new Edge(currentPoint, midPoint);
//Check if this line is intersecting
bool canSeeEdge = true;
for (int k = 0; k < edges.Count; k++)
{
//Dont compare the edge with itself
if (k == j)
{
continue;
}
if (AreEdgesIntersecting(edgeToMidpoint, edges[k]))
{
canSeeEdge = false;
break;
}
}
//This is a valid triangle
if (canSeeEdge)
{
Edge edgeToPoint1 = new Edge(currentEdge.v1, new Vertex(currentPoint));
Edge edgeToPoint2 = new Edge(currentEdge.v2, new Vertex(currentPoint));
newEdges.Add(edgeToPoint1);
newEdges.Add(edgeToPoint2);
Triangle newTri = new Triangle(edgeToPoint1.v1, edgeToPoint1.v2, edgeToPoint2.v1);
triangles.Add(newTri);
}
}
for (int j = 0; j < newEdges.Count; j++)
{
edges.Add(newEdges[j]);
}
}
return triangles;
}
private static bool AreEdgesIntersecting(Edge edge1, Edge edge2)
{
Vector2 l1_p1 = new Vector2(edge1.v1.position.x, edge1.v1.position.z);
Vector2 l1_p2 = new Vector2(edge1.v2.position.x, edge1.v2.position.z);
Vector2 l2_p1 = new Vector2(edge2.v1.position.x, edge2.v1.position.z);
Vector2 l2_p2 = new Vector2(edge2.v2.position.x, edge2.v2.position.z);
bool isIntersecting = Intersections.AreLinesIntersecting(l1_p1, l1_p2, l2_p1, l2_p2, true);
return isIntersecting;
}
}
And this is the final triangulation:
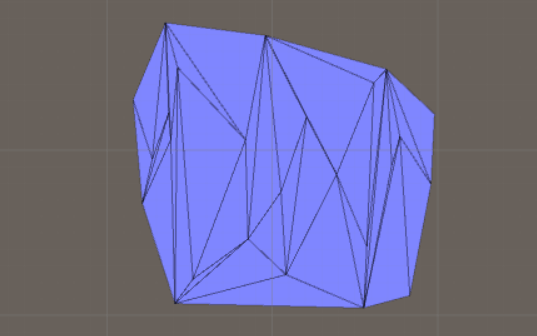
If you want to produce triangulations that look better you have to learn the Delaunay triangulation algorithm, which is the topic of another section of this tutorial.