What if you have several random points and want to find the smallest shape that's enclosing these points. This shape is called a convex hull, and there are several algorithms you can use to find this convex hull. You can find them here: Convex hull algorithms.
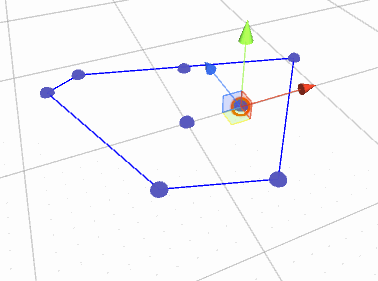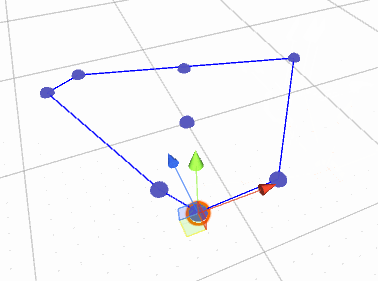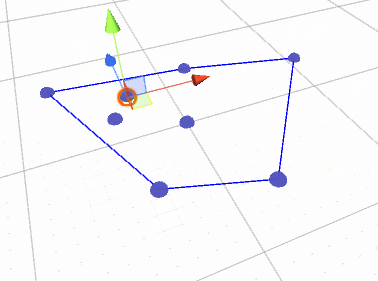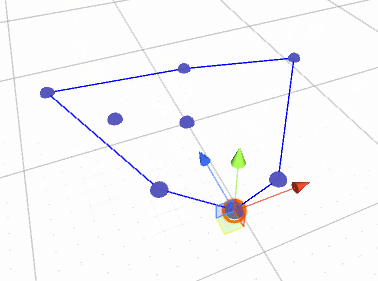
We are here going to use the Gift wrapping algorithm, also known as a Jarvis March. This is the simplest convex hull algorithm, but will it also take the longest time to generate the convex hull? In some cases yes. But in some cases this algorthm is fast if not all points are on the convex hull. Faster algorithms tend to be more complicated if you have colinear points, while the Jarvis March algorithm will be able to deal with colinear points and other numerical difficulties without any problems. So the algortihm is sometimes slow, but robust.
This is how the algorithm works. Step 1 is to sort all vertices to figure out which one has the smallest x coordinate, and if there are multiple points with the smallest x coordinate, we pick the point with the smallest x and z coordinate. This point is always on the convex hull. Step 2 is to loop through all other points to identify which points are on the convex hull. To know if two points are on the convex hull, we have to check all other points and make sure none of them are to the right of a line between the two points. If you are confused, you should look at this YouTube video.
To make all this work in Unity you need random points in x-z-space and they should be stored as a Vertex in a list (Create a new Vertex object with a Vector3 as its position and where y = 0). You also need an algorithm to figure out if a point is to the left, to the right, or on the same line as 2 other points.
using System.Collections;
using System.Collections.Generic;
using System.Linq;
using UnityEngine;
//Generate a counter-clockwise convex hull with the jarvis march algorithm (gift wrapping)
//The algorithm is O(n*n) but is often faster if the number of points on the hull is fewer than all points
//In that case the algorithm will be O(h * n)
//Is more robust than other algorithms because it will handle colinear points with ease
//The algorithm will fail if we have more than 3 colinear points
//But this is a special case, which will take time to test, so make sure they are NOT colinear!!!
public static class JarvisMarchAlgorithm
{
public static List<Vertex> GetConvexHull(List<Vertex> points)
{
//If we have just 3 points, then they are the convex hull, so return those
if (points.Count == 3)
{
//These might not be ccw, and they may also be colinear
return points;
}
//If fewer points, then we cant create a convex hull
if (points.Count < 3)
{
return null;
}
//The list with points on the convex hull
List<Vertex> convexHull = new List<Vertex>();
//Step 1. Find the vertex with the smallest x coordinate
//If several have the same x coordinate, find the one with the smallest z
Vertex startVertex = points[0];
Vector3 startPos = startVertex.position;
for (int i = 1; i < points.Count; i++)
{
Vector3 testPos = points[i].position;
//Because of precision issues, we use Mathf.Approximately to test if the x positions are the same
if (testPos.x < startPos.x || (Mathf.Approximately(testPos.x, startPos.x) && testPos.z < startPos.z))
{
startVertex = points[i];
startPos = startVertex.position;
}
}
//This vertex is always on the convex hull
convexHull.Add(startVertex);
points.Remove(startVertex);
//Step 2. Loop to generate the convex hull
Vertex currentPoint = convexHull[0];
//Store colinear points here - better to create this list once than each loop
List<Vertex> colinearPoints = new List<Vertex>();
int counter = 0;
while (true)
{
//After 2 iterations we have to add the start position again so we can terminate the algorithm
//Cant use convexhull.count because of colinear points, so we need a counter
if (counter == 2)
{
points.Add(convexHull[0]);
}
//Pick next point randomly
Vertex nextPoint = points[Random.Range(0, points.Count)];
//To 2d space so we can see if a point is to the left is the vector ab
Vector2 a = currentPoint.GetPos2D_XZ();
Vector2 b = nextPoint.GetPos2D_XZ();
//Test if there's a point to the right of ab, if so then it's the new b
for (int i = 0; i < points.Count; i++)
{
//Dont test the point we picked randomly
if (points[i].Equals(nextPoint))
{
continue;
}
Vector2 c = points[i].GetPos2D_XZ();
//Where is c in relation to a-b
// < 0 -> to the right
// = 0 -> on the line
// > 0 -> to the left
float relation = Geometry.IsAPointLeftOfVectorOrOnTheLine(a, b, c);
//Colinear points
//Cant use exactly 0 because of floating point precision issues
//This accuracy is smallest possible, if smaller points will be missed if we are testing with a plane
float accuracy = 0.00001f;
if (relation < accuracy && relation > -accuracy)
{
colinearPoints.Add(points[i]);
}
//To the right = better point, so pick it as next point on the convex hull
else if (relation < 0f)
{
nextPoint = points[i];
b = nextPoint.GetPos2D_XZ();
//Clear colinear points
colinearPoints.Clear();
}
//To the left = worse point so do nothing
}
//If we have colinear points
if (colinearPoints.Count > 0)
{
colinearPoints.Add(nextPoint);
//Sort this list, so we can add the colinear points in correct order
colinearPoints = colinearPoints.OrderBy(n => Vector3.SqrMagnitude(n.position - currentPoint.position)).ToList();
convexHull.AddRange(colinearPoints);
currentPoint = colinearPoints[colinearPoints.Count - 1];
//Remove the points that are now on the convex hull
for (int i = 0; i < colinearPoints.Count; i++)
{
points.Remove(colinearPoints[i]);
}
colinearPoints.Clear();
}
else
{
convexHull.Add(nextPoint);
points.Remove(nextPoint);
currentPoint = nextPoint;
}
//Have we found the first point on the hull? If so we have completed the hull
if (currentPoint.Equals(convexHull[0]))
{
//Then remove it because it is the same as the first point, and we want a convex hull with no duplicates
convexHull.RemoveAt(convexHull.Count - 1);
break;
}
counter += 1;
}
return convexHull;
}
}
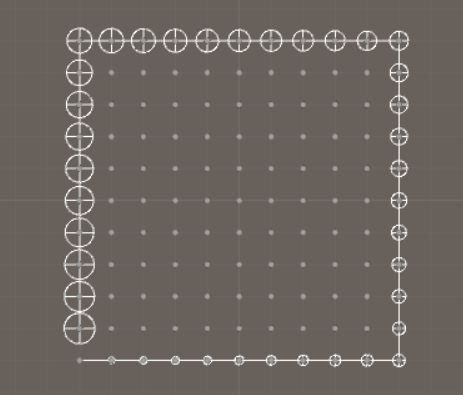
It should look like this in Unity if you have 200 random points:

...or colinear points: