
You have two line segments and want to know if they are crossing each other:


This is more complicated than it seems, but you can probably ignore some steps depending on which application you are making. For example, it's often unnecessary to test if the line segments are parallel if you are making a game, because the probability that they are exactly parallel is low.
using UnityEngine;
using System.Collections;
namespace LinearAlgebra
{
//How to figure out if two lines are intersecting
public class LineLineIntersection : MonoBehaviour
{
//The start end of each line
public Transform L1_start;
public Transform L1_end;
public Transform L2_start;
public Transform L2_end;
//Just attach a line renderer to an empty game object
public LineRenderer lineRenderer1;
public LineRenderer lineRenderer2;
void Start()
{
//Give the line renderer a material so we can change the color if they intersect
lineRenderer1.material = new Material(Shader.Find("Unlit/Color"));
lineRenderer2.material = new Material(Shader.Find("Unlit/Color"));
}
void Update()
{
//Connect the points with line renderers
lineRenderer1.SetPosition(0, L1_start.position);
lineRenderer1.SetPosition(1, L1_end.position);
lineRenderer2.SetPosition(0, L2_start.position);
lineRenderer2.SetPosition(1, L2_end.position);
//Set the default color
lineRenderer1.material.color = Color.red;
lineRenderer2.material.color = Color.red;
//Change color if they intersect
if (IsIntersecting())
{
lineRenderer1.material.color = Color.blue;
lineRenderer2.material.color = Color.blue;
}
}
//Check if the lines are interesecting in 2d space
bool IsIntersecting()
{
bool isIntersecting = false;
//3d -> 2d
Vector2 l1_start = new Vector2(L1_start.position.x, L1_start.position.z);
Vector2 l1_end = new Vector2(L1_end.position.x, L1_end.position.z);
Vector2 l2_start = new Vector2(L2_start.position.x, L2_start.position.z);
Vector2 l2_end = new Vector2(L2_end.position.x, L2_end.position.z);
//Direction of the lines
Vector2 l1_dir = (l1_end - l1_start).normalized;
Vector2 l2_dir = (l2_end - l2_start).normalized;
//If we know the direction we can get the normal vector to each line
Vector2 l1_normal = new Vector2(-l1_dir.y, l1_dir.x);
Vector2 l2_normal = new Vector2(-l2_dir.y, l2_dir.x);
//Step 1: Rewrite the lines to a general form: Ax + By = k1 and Cx + Dy = k2
//The normal vector is the A, B
float A = l1_normal.x;
float B = l1_normal.y;
float C = l2_normal.x;
float D = l2_normal.y;
//To get k we just use one point on the line
float k1 = (A * l1_start.x) + (B * l1_start.y);
float k2 = (C * l2_start.x) + (D * l2_start.y);
//Step 2: are the lines parallel? -> no solutions
if (IsParallel(l1_normal, l2_normal))
{
Debug.Log("The lines are parallel so no solutions!");
return isIntersecting;
}
//Step 3: are the lines the same line? -> infinite amount of solutions
//Pick one point on each line and test if the vector between the points is orthogonal to one of the normals
if (IsOrthogonal(l1_start - l2_start, l1_normal))
{
Debug.Log("Same line so infinite amount of solutions!");
//Return false anyway
return isIntersecting;
}
//Step 4: calculate the intersection point -> one solution
float x_intersect = (D * k1 - B * k2) / (A * D - B * C);
float y_intersect = (-C * k1 + A * k2) / (A * D - B * C);
Vector2 intersectPoint = new Vector2(x_intersect, y_intersect);
//Step 5: but we have line segments so we have to check if the intersection point is within the segment
if (IsBetween(l1_start, l1_end, intersectPoint) && IsBetween(l2_start, l2_end, intersectPoint))
{
Debug.Log("We have an intersection point!");
isIntersecting = true;
}
return isIntersecting;
}
//Are 2 vectors parallel?
bool IsParallel(Vector2 v1, Vector2 v2)
{
//2 vectors are parallel if the angle between the vectors are 0 or 180 degrees
if (Vector2.Angle(v1, v2) == 0f || Vector2.Angle(v1, v2) == 180f)
{
return true;
}
return false;
}
//Are 2 vectors orthogonal?
bool IsOrthogonal(Vector2 v1, Vector2 v2)
{
//2 vectors are orthogonal is the dot product is 0
//We have to check if close to 0 because of floating numbers
if (Mathf.Abs(Vector2.Dot(v1, v2)) < 0.000001f)
{
return true;
}
return false;
}
//Is a point c between 2 other points a and b?
bool IsBetween(Vector2 a, Vector2 b, Vector2 c)
{
bool isBetween = false;
//Entire line segment
Vector2 ab = b - a;
//The intersection and the first point
Vector2 ac = c - a;
//Need to check 2 things:
//1. If the vectors are pointing in the same direction = if the dot product is positive
//2. If the length of the vector between the intersection and the first point is smaller than the entire line
if (Vector2.Dot(ab, ac) > 0f && ab.sqrMagnitude >= ac.sqrMagnitude)
{
isBetween = true;
}
return isBetween;
}
}
}
The above version is more robust and will even work in more dimensions, but if speed is the key and you are working in 2d space, I've found another solution here. So you can replace the fat version with this:
//Check if the lines are interescting in 2d space
//Alternative version from http://thirdpartyninjas.com/blog/2008/10/07/line-segment-intersection/
bool IsIntersectingAlternative()
{
bool isIntersecting = false;
//3d -> 2d
Vector2 p1 = new Vector2(L1_start.position.x, L1_start.position.z);
Vector2 p2 = new Vector2(L1_end.position.x, L1_end.position.z);
Vector2 p3 = new Vector2(L2_start.position.x, L2_start.position.z);
Vector2 p4 = new Vector2(L2_end.position.x, L2_end.position.z);
float denominator = (p4.y - p3.y) * (p2.x - p1.x) - (p4.x - p3.x) * (p2.y - p1.y);
//Make sure the denominator is > 0, if so the lines are parallel
if (denominator != 0)
{
float u_a = ((p4.x - p3.x) * (p1.y - p3.y) - (p4.y - p3.y) * (p1.x - p3.x)) / denominator;
float u_b = ((p2.x - p1.x) * (p1.y - p3.y) - (p2.y - p1.y) * (p1.x - p3.x)) / denominator;
//Is intersecting if u_a and u_b are between 0 and 1
if (u_a >= 0 && u_a <= 1 && u_b >= 0 && u_b <= 1)
{
isIntersecting = true;
}
}
return isIntersecting;
}
But sometimes we may run into floating point precision issues. To solve that, a common way is to add a small epsilon so we never compare with for example exactly 0.
public static bool AreLinesIntersecting(Vector2 l1_p1, Vector2 l1_p2, Vector2 l2_p1, Vector2 l2_p2, bool shouldIncludeEndPoints)
{
//To avoid floating point precision issues we can add a small value
float epsilon = 0.00001f;
bool isIntersecting = false;
float denominator = (l2_p2.y - l2_p1.y) * (l1_p2.x - l1_p1.x) - (l2_p2.x - l2_p1.x) * (l1_p2.y - l1_p1.y);
//Make sure the denominator is > 0, if not the lines are parallel
if (denominator != 0f)
{
float u_a = ((l2_p2.x - l2_p1.x) * (l1_p1.y - l2_p1.y) - (l2_p2.y - l2_p1.y) * (l1_p1.x - l2_p1.x)) / denominator;
float u_b = ((l1_p2.x - l1_p1.x) * (l1_p1.y - l2_p1.y) - (l1_p2.y - l1_p1.y) * (l1_p1.x - l2_p1.x)) / denominator;
//Are the line segments intersecting if the end points are the same
if (shouldIncludeEndPoints)
{
//Is intersecting if u_a and u_b are between 0 and 1 or exactly 0 or 1
if (u_a >= 0f + epsilon && u_a <= 1f - epsilon && u_b >= 0f + epsilon && u_b <= 1f - epsilon)
{
isIntersecting = true;
}
}
else
{
//Is intersecting if u_a and u_b are between 0 and 1
if (u_a > 0f + epsilon && u_a < 1f - epsilon && u_b > 0f + epsilon && u_b < 1f - epsilon)
{
isIntersecting = true;
}
}
}
return isIntersecting;
}
There's actually a third way to figure out if two line segments in 2d space are intersecting. The problem with this way is that you can't find the point of intersection, but that doesn't matter if you don't need to. To help us we are going to use the dot product! The basic idea is this (we want to see if the blue line and the black line is intersecting):
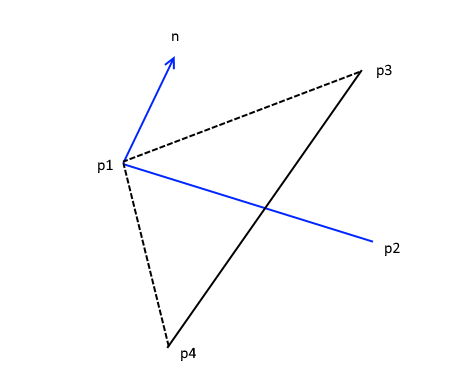
We first have to find the normal to a line. Then we calculate the dot product between this normal and the direction between the normal and the two points on the other line. If one of these dot products is negative and the other is positive, then we know the points on the other line are on different sides of the first line. Then we repeat the process for the other line. If you want a more detailed explanation you should watch this video: TypeScript Game Development - Basic 2D Collision Detection. The code looks like this:
//Line segment-line segment intersection in 2d space by using the dot product
//p1 and p2 belongs to line 1, and p3 and p4 belongs to line 2
public static bool AreLineSegmentsIntersectingDotProduct(Vector3 p1, Vector3 p2, Vector3 p3, Vector3 p4)
{
bool isIntersecting = false;
if (IsPointsOnDifferentSides(p1, p2, p3, p4) && IsPointsOnDifferentSides(p3, p4, p1, p2))
{
isIntersecting = true;
}
return isIntersecting;
}
//Are the points on different sides of a line?
private static bool IsPointsOnDifferentSides(Vector3 p1, Vector3 p2, Vector3 p3, Vector3 p4)
{
bool isOnDifferentSides = false;
//The direction of the line
Vector3 lineDir = p2 - p1;
//The normal to a line is just flipping x and z and making z negative
Vector3 lineNormal = new Vector3(-lineDir.z, lineDir.y, lineDir.x);
//Now we need to take the dot product between the normal and the points on the other line
float dot1 = Vector3.Dot(lineNormal, p3 - p1);
float dot2 = Vector3.Dot(lineNormal, p4 - p1);
//If you multiply them and get a negative value then p3 and p4 are on different sides of the line
if (dot1 * dot2 < 0f)
{
isOnDifferentSides = true;
}
return isOnDifferentSides;
}
So which one is the fastest? I've used C#'s stopwatch timer to measure the time of the three line segment-line segment algorithms, and after 1000 updates, this was the total time: