Minimize an error with a PID controller in Unity with C#

This is a tutorial on how you can minimize an error with the help of a PID controller. This is a technique used in real-life Control Theory.

So what's a PID controller. A PID controller consists of three parts:

1. P - Proportional
2. I - Integral
3. D - Derivative

...which can be summarized in a rather scary equation:

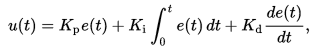
But this equation becomes just a few lines of code. The first part is the P, which is simply just a multiplication of the error you want to minimize with a constant you have to determine. These constants (Kp, Ki, and Kd) are called gains. If we just have the P part of the PID controller, the result is a drunk (oscillating) behavior:

To avoid this drunk behavior, we need the D part of the equation. This D is simply the difference between the current error and the error last time step divided by the time step, and you multiply this with another constant of your choice. This will make the car smooth in to the correct direction:

The last part of the PID controller is the I. This is simply the sum of all previous errors multiplied with a third constant of your choice. The idea behind the I part is that if the car has a built-in error in itself (real-life technology is not as accurate as in the computer) the I will minimize this error. The other idea is that if the error is large, the PID controller will make the machine move faster and faster to minimize the error. So you can often avoid the I part if you want, and then the controller is called PD. Anyway, if all this is abstract, I've made a youtube video that will show why we need the PID controller:

How do you determine the gains Kp, Ki, and Kd? You can experiment to find the three gains. But there's actually a way to generate these constants called Twiddle, but I've found it's easier to test different values.

What will you learn?

1. Improve the steering of a self-driving car
2. Stabilize a Segway
3. Stabilize and fly around with a quadcopter

Back